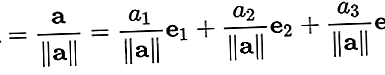Vectorul în matematică și fizică poate fi definit ca obiecte geometrice care au magnitudine și direcție. Vectorul este descris cu o săgeată, unde baza săgeții arată un punct de prindere (punctul de plecare) al unui vector, lungimea săgeții indică dimensiunea sau valoarea vectorului (cu cât săgeata este mai lungă, cu atât este mai mare valoarea sau valoarea vectorului și invers), în timp ce săgeata indică direcția vectorului.

În scris, dacă vectorul începe la punctul A și se termină la punctul B, atunci poate fi scris într-o mică literă deasupra căreia există o linie / săgeată ca 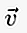 sau
sau 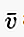 sau, de asemenea:
sau, de asemenea:
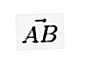
Tipuri de vectori
Vectorul în matematică este împărțit în 4 tipuri, inclusiv:
Vector de poziție
Un vector al cărui punct de pornire este la 0 (0,0) și al cărui final este A (a1, a2).
Vector zero
„Vector zero” (vector nul sauvector zero) este un vector a cărui lungime este „zero”. Scrierea în această coordonată vectorială este (0,0,0) și de obicei i se dă un simbol  , sau0. Acest vector diferă de alți vectori prin faptul că nu poate fi normalizat (adică niciun vector unitar nu este multiplu al vectorului zero). Numărul de vectori este zero cu orice vectorA esteA (acesta este,0+A=A).
, sau0. Acest vector diferă de alți vectori prin faptul că nu poate fi normalizat (adică niciun vector unitar nu este multiplu al vectorului zero). Numărul de vectori este zero cu orice vectorA esteA (acesta este,0+A=A).
Vectorul zero nu are o direcție clară a vectorului.
Vector de unitate
este un vector cu lungimea „unu”. De obicei vectorul unitar este folosit doar pentru a indica direcția. Un vector de orice lungime poate fi împărțit la lungime pentru a obține vectorul unitar. Acest lucru este cunoscut sub numele de „normalizarea” unui vector. Un vector unitate este adesea indicat printr-un „capac” peste litera mică „a” ca înA.
Pentru a normaliza un vectorA = [A1, A2, A3], împarte vectorul la lungimea ||A||. Asa de:
Vector de bază
Un vector unitate care este perpendicular unul pe celălalt. Într-un vector spațial bidimensional (R2) are doi vectori de bază și anume 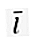 = (1, 0) și
= (1, 0) și 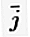 = (0, 1).
= (0, 1).
Asemănarea a doi vectori
Se spune că doi vectori sunt aceiași dacă au aceeași lungime și direcție

O aliniere a doi vectori
Doi vectori sunt numiți paraleli (paraleli) dacă linia care reprezintă cei doi vectori este paralelă.
Operații vectoriale
Înmulțirea scalară
Un vector poate fi multiplicat cu un scalar care are ca rezultat și un vector, vectorul rezultat fiind:
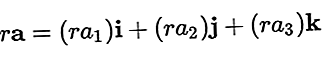
Adunarea vectorului și scăderea vectorului
Ca exemplu de vector A=A1eu + A2j + A3k șib=b1eu + b2j + b3k
Rezultatul unui plus b este: 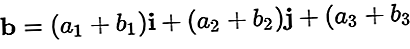
reducerea vectorului se aplică și prin înlocuirea semnului + într-un semn -